S

Scaling up describes the efficiency improvement of two geometrically similar centrifugal pumps (e.g. model, prototype) as a result of an increase in the Reynolds number and/or a decrease of the relative surface roughness (see also Efficiency scale-up).

A screw pump is a rotary positive displacement pump with two intermeshing counter-rotating screws which simultaneously serve as displacement bodies and separating elements.

Sealing elements, or seals, are components or constructions which help to limit or prevent the unintentional transition of substances from one space to another.

Sealing elements in centrifugal pumps are designed to ensure the separation of internal and external spaces within and around the pump in a leaktight manner, or with minimal leakage. Sealing elements are still referred to as sealing elements even if absolute leak tightness is not achieved (e.g. in the case of throttling). Degrees of sealing range from absolutely leak-tight sealing elements (welding together of sealing faces), to non-welded sealing elements (e.g. gaskets, ground sealing elements, O-rings) and clearance gap constructions with a given leakage rate.

A large number of different sealing methods and elements (from elements sealing off the pump connection to the piping to diverse internal pump seals) are available to provide solutions which meet the numerous requirements of pumping applications.

Sealing element types

• Stationary mating sealing faces
• Sealing faces which slide against one another
• Sealing faces which adjust themselves in relation to one another within given limits
• Sealing faces which rotate against one another

Centrifugal pumps are mostly connected to the piping by means of sealing elements with stationary mating sealing faces, although other seal types are also used (sealing elements whose faces adjust themselves in relation to one another within given limits and whose sealing faces rotate against one another).

Stationary mating sealing faces

Sealing element designs must be selected according to the functions stationary mating sealing faces are required to perform (i.e. "sealing", "centring" or "aligning"). Considerable forces are often necessary to perform the "sealing" function. The axial contact pressure required by axially sealing O-rings is relatively low; axially sealing gaskets necessitate more, and the highest contact pressure is required by sealing elements with ground metal sealing faces. Radially sealing O-rings, by contrast, require only a low radial preloading force for the sealing function.

Sealing elements at locations such as drain plugs function only to seal, and can therefore be very flexible because they perform no alignment function. Sealing elements which are not exposed to a significant differential pressure, e.g. at bearing covers of bearing brackets, can employ a simple design.

Rotating seals fitted between stationary sealing faces (e.g. shaft protecting sleeve against shaft) are subjected to both centrifugal and differential pressure forces. A suitable design (e.g. confined gaskets) ensures that these can be absorbed.

Differentiation between sealing elements with stationary mating sealing faces:

• Non-separable (welded flanges and sealing faces)
• Separable (gaskets, flexible materials)
• Confined (O-rings etc.)
• Lens gasket (metal sealing elements)
• Sealing elements fed with barrier fluid (for toxic or explosive fluids, or if there is a risk of air penetrating at pressures below atmosphere)

Sealing faces which slide against one another 

Sealing faces which slide against one another are used to compensate for thermal expansion during installation or operation due to temperature fluctuations, an example being two concentric pipes sealed against one another by a gland packing. In the case of mechanical seals, compensation for the seals' axial movement is ensured by means of O-rings or rubber bellows.

Sealing faces which adjust themselves in relation to one another within given limits

Sealing faces which adjust themselves in relation to one another within given limits are sealed by means of diaphragms, bellows and expansion joints (to limit the forces acting on the nozzles or to provide noise insulation between the pump casing and the piping). This type of sealing element also includes the connection and sealing by hoses.

Sealing faces which rotate against one another

In the case of sealing faces which rotate against one another, the task is to seal rotating machine components against non-rotating parts in such a way that leakage or the penetration of substances from the outside are reduced to a given extent and possible wear of the sealing faces is minimised (See also Shaft seal).

From a chemical perspective, seawater is a saline, aqueous solution. The salinity of individual seas varies from 0.3 to 1.7 % (Baltic Sea) to 28 % (Dead Sea). The sea salt contained in seawater consists mainly of sodium chloride (common salt). Sea salt also contains magnesium chloride, magnesium sulphate, calcium sulphate, potassium chloride and calcium carbonate, and traces of other salts (also see Chemical resistance table).

A seawater desalination system is a facility for producing drinking water or service water from seawater.

Seawater desalination has been gaining increasingly in importance in recent years. There are a number of processes that can convert the feed water pumped from the sea into desalinated water which can be used as drinking water, for example, after suitable treatment. Because of the high amount of energy required, seawater desalination is only worthwhile in places where fresh water is in short supply, for example on islands or ships.

Seawater desalination processes 

• Distillation processes
• Freezing processes
• Solvent extraction
• Reverse osmosis
• Electrodialysis
• Ion exchange processes

Seawater desalination processes of technical and practical importance include the RO (reverse osmosis) process and the MSF distillation process.

MSF process

MSF stands for multi-stage-flash, a process in which the feed water extracted from the sea gradually gradually warms up as it passes through the condenser coils (heat exchangers) of each individual stage. See Fig. 1 Seawater desalination system

After leaving stage 1, the temperature of the feed water is increased still further in the brine heater, as a further heat exchanger. This brine heater may receive its heat energy from the waste steam of the process plant connected to the seawater desalination system or of the power station (e.g. a coal-fired power station).

The brine, which is now at a high temperature, then flows through the evaporation chambers of stages 1 to 10, releasing vapour. The vapour rises through the demisting device of each stage and condenses on the condenser coils. The condensed water (distillate) is collected in the tanks situated beneath the coils and is fed away for further treatment after the final stage.

The pressure is further decreased from one stage to the next, whereby the temperature of the brine decreases and the salt concentration increases.

This method generally relies on the following centrifugal pumps: the tubular casing pump as a brine recirculation and cooling water pump, the volute casing pump in back pull-out design as a distillate and decarbonisation pump, the doubleentry volute casing pump as a brine blowdown pump, and the vertical condensate pump. 

RO process

RO stands for reverse osmosis.

The reverse osmosis process rests on the following principle: with aqueous salt solutions having different concentrations separated by a semi-permeable membrane, the water from the solution with the lower concentration penetrates the membrane into the region of the higher concentration (osmosis). This process continues until an equilibrium has been attained between the two concentrations and until a given pressure (osmotic pressure) has built up on the side of the higher concentration.

If the pressure on the side of the higher concentration is increased to a value above that of the osmotic pressure, the process will occur in the reverse direction (reverse osmosis). High-purity water with only a very low salt content will penetrate through the membrane from the high concentration salt solution.

This water (permeate) can be used as drinking water, whilst a concentrated salt solution is left on the high-pressure side of the membrane. See Fig. 2 Seawater desalination system

Modern seawater desalination systems operate according to the reverse osmosis principle, in which pressure higher than the naturally occurring osmotic pressure is applied to push salt water through a membrane that is permeable only to the water molecules. This is done by channelling seawater under pressure past the membrane, whereby a proportion of the water passes through the membrane and the remaining seawater (brine) is concentrated. The proportion of the water diffused through the membrane is approximately 40 % of the seawater used. The remaining 60 % of concentrated brine is discharged as reject stream.

The pressure drop across the osmotic membrane is independent of the ratio of the salt concentrations on the two sides of the membrane. If this pressure is 65 bar, this results in irrecoverable energy loss (W) of 1.76 kWh/m³ of desalinated water. However, most of the energy contained in the brine can be recovered.

Taking all efficiency losses of the RO system into account, energy input of at least 2.5 to 5 kW/m³ must be expected. The actual energy input is therefore dependent both on the quality of the recovery of the energy contained in the discharged seawater, and on the efficiency of the pumps and systems used for pressure generation and for auxiliary processes.

The basic structure of an RO system is the same for all system types, the main difference being the type of energy recovery.

One option for energy recovery is to release the brine pressure via a turbine and return the shaft power of the turbine to the pump shaft. See Fig. 3 Seawater desalination system

The most energy-efficient option for energy recovery is to use a pressure exchanger, in which the pressure of the brine is transferred directly to the feed water do be desalinated. See Fig. 4 Seawater desalination system

All systems are equipped with different pumps depending on their design. These pumps must all be built using stainless materials because of the salt water to be handled. This also applies for valves.

Energy recovery is often dispensed with in small installations because of the high system cost. In this case the pressure is reduced, mainly unused, via a throttle valve.

Such installations are usually equipped with only one high-pressure pump. In addition to multistage centrifugal pumps, piston pumps/plunger pumps are also used here. See Fig. 5 Seawater desalination system

Larger installations usually have several pumps. For example, the salt water for the plant is transferred from a reservoir using a booster pump, which may be a borehole pump or other type for a different extraction method.
The salt water is pumped through a filter to remove solid substances and suspended particles. A high-pressure pump installed downstream of the filter generates the osmotic pressure for the osmotic membrane.

Plants with a pressure exchanger also require a circulating pump, which is used for overcoming inner losses in the membrane, valves and the pressure exchanger. It is also a single-stage centrifugal pump with a head of approx. 30 m, which must be designed for the system pressure of the feed pump. The feed pump is always a multistage centrifugal pump, which is designed with few stages in accordance with its head of approx. 650 m.

Seawater pumps are centrifugal pumps for seawater used for cooling purposes (see Marine pump) made of materials resistant to seawater (see Chemical resistance table).

A selection chart is a graphic representation of the characteristic curves selection charts of several pump sizes and types in a common H/Q diagram (flow rate and head).

In normal conditions, common centrifugal pumps are unable to evacuate the air from an inlet line leading to a fluid level whose geodetic altitude is below that of the pump. Self-priming pumps have to be capable of evacuating air (see Venting) from the pump suction line without any external auxiliary devices.

Centrifugal pumps with an internal suction stage such as water jet pumps or side channel pumps are also classified as self-priming pumps.

Centrifugal pumps which are not designed with an internal or external self-priming stage can only start to pump the fluid after the pump has initially been primed with the fluid. In addition, a suction-side swing check valve or a vent valve must be fitted to prevent any siphon action and ensure that the fluid remains in the casing when the pump has been stopped. In self-priming centrifugal pumps with a separation chamber the fluid pumped and the entrained air bubbles are pumped into the separation chamber by the impeller action. See Fig. 1 Self-priming pump

The air escapes through the pump discharge nozzle whilst the fluid drops back down and is once more entrained by the impeller. The suction line is thus continuously evacuated. The design required for such a self-priming feature has an adverse effect on pump efficiency. Also, the dimensions of the separating chamber are relatively large. For these reasons this solution is only adopted for small pumps, e.g. garden pumps. More frequently used types of self-priming pumps are side channel and water ring pumps. Another type of self-priming pump is a centrifugal pump with two casing chambers and an open impeller. This design is not only used for its self-priming capabilities but also for its degassing effects when pumping twophase mixtures (air/gas and liquid) for a short time in process engineering or when handling polluted fluids, for example when draining water from construction pits. See Fig. 2 Self-priming pump

This pump type operates without a foot valve and without an evacuation device on the suction side. The pump has to be primed with the fluid to be handled prior to commissioning. See Fig. 3 Self-priming pump

Two-phase mixture is pumped until the suction line has been evacuated and the fluid level has been pushed into the front suction intake chamber or atmospheric pressure. During normal pumping operation this pump works like an ordinary centrifugal pump. See Figs. 4, 5 Self-priming pump

Self-regulation is a type of closed-loop control, whereby the H/Q curve is changed by self-regulating the flow rate in line with the suction head (see Suction characteristics) as a result of cavitation (see Condensate pump).

A sensor is also referred to as a transmitter or pick-up and qualitatively or quantitatively (as values) records specific (physical or chemical) properties of its environment as a technical component, whereby variables not suitable as signals are converted to signals designated for further processing.

Sensor classification based on energy usage

• Active sensor: Active sensors do not require a power source. They provide a signal in the form of an electrical voltage, charge, or current such that only changes in the measurand can be determined.
• Passive sensor: Passive sensors change an electrical parameter such as resistance, capacity, or inductivity and require a power source for this purpose. This also enables the measurement of static or quasi-static measurands and is the reason why these sensors are typically used.
• Optical sensor: Optical sensors transform non-optical variables into optical signals, which are subsequently processed further by opto-electronic devices. 

Sensors (measuring elements) differ according to their measuring principle.

Measuring principles

• Differential transformer, e.g. displacement sensor 
• Inductive sensor, e.g. valve disc positioning
• Capacitive sensor, e.g. pressure or level measurement
• Bubbler control,  e.g. level measurement in waste water plant
• Magnetic field measurement, e.g. distance measurement as proximity sensor
• Magneto-elastic measurement, e.g. torque or force measurement 
• MIF (Magnetic-Inductive Flow measurement)
• Opto-electronic sensor, e.g. light barrier
• Piezoelectric sensor, e.g. pressure, oscillation, and force measurement
• Resistive sensor, e.g. strain gauge
• Temperature sensor, e.g. PT 100
• Thermoelectric principle, e.g. temperature measurement
• Eddy current sensor, e.g. layer thickness measurement

Configured (selected) sensors

• Absolute pressure sensor, e.g. air pressure measurement
• Differential pressure sensor
• NTC thermistor (see NTC resistor), e.g. temperature measurement
• Inductive proximity sensor, e.g. non-contact displacement/position measurement
• Inductive displacement sensor, e.g. displacement/position measurement
• PTC thermistor (see PTC resistor), e.g. temperature measurement
• Level, e.g. water, fill, sound, signal, and voltage levels
• Float switch, e.g. dry running protection for submersible motor pump
• Thermocouple, e.g. temperature measurement

If the sensors are equipped with integrated measured value conditioning, they are referred to as sensor systems.

Series operation means that pumps are connected and started one after another, i. e. in series. This type of operation has many advantages over parallel operation in cases where the system characteristic curve H_sys(Q) is steep and the pump characteristic curve H_I+II(Q) is flat (see Characteristic curve). The addition of the head values of pumps operating in series is better suited to the steep system characteristic curve than the addition of the flow rates in parallel operation. When two centrifugal pumps (I and II) are operating in series, the head (H_I+II) is the sum of the individual pumps' heads and the flow rate remains the same.

The characteristics of series operation are easier to understand than those for parallel operation and are not complicated by unstable H/Q curves or varying shut-off heads. See Fig. 1 Series operation

When several centrifugal pumps are operated in series, the pump casings and shaft seals of the next pump in series need to be sufficiently sized to withstand the higher pressure. The pump with the best suction characteristics should be placed in the lead position.

When starting up (see Start-up process) the lead pump must generate enough pressure to eliminate the risk of cavitation before the next pump can be started up. When shutting down, no pump on a lower pressure level may be stopped as long as the next pump in series is still running, otherwise the flow will run through the non-driven pump as through a rotating throttle which will drive the available NPSHA (net positive suction head) for the next pump in series down to an unacceptable level. It is sometimes necessary to interlock the drives.

After changing a pump system from single-pump to series operation, not only the head but also the flow rate in each of the pumps connected in series is enlarged. When selecting the pumps, it is therefore necessary to ensure that the NPSHR (net positive suction head required by the pump) is sufficient.

If the above mentioned conditions are observed and it can be ensured that the non-driven pump is either not rotated by the fluid flow or bypassed during its standstill, then series operation is suitable for economic, stepwise control of centrifugal pumps.

If stepwise start-up and stopping of the pumps as described above is not required, it is easier and less expensive to use multistage pumps in which the impellers and diffusers are arranged in a common pump casing instead of using several centrifugal pumps in series operation (see Multistage pump).

Series-produced pumps are pumps that are manufactured in series rather than undergoing customised production.

Service water designates water used for purposes other than drinking. It is intended for specific applications and must comply with their technological requirements (e. g. decalcified cooling water).

A service water pump is a pump employed to handle service water used in industrial processes. It is used in both open systems (e.g. in wells, rivers, lakes) and closed systems (e.g. cooling water in recycling processes).

The design and operating limits are identical to those of water supply pumps.

Single-pump or dual-pump sewage lifting units are used in buildings, including hotels and hospitals, to dispose of domestic waste water and sewage from below the flood level, where it will not run off following a natural gradient. In these cases free-flow impellers are the most common type of impeller.
See Fig. 1 Sewage pump

In refurbished buildings, waste water also needs to be disposed of from above the flood level. To be able to discharge the waste water into the sewer system through small diameter pipelines, the pipe inlet is fitted with cutters or other macerators to reduce the size of solid particles.

Sewage lifting units are complete drainage systems which operate automatically. Water level sensors are integrated in the collecting tank to monitor and control the pumps in combination with a control system. The pumps are started and stopped as a function of the water level.

In small sewage lifting units, the hydraulic system is installed inside the tank; in large units it is installed outside the tank. Sewage lifting units are driven by surface-cooled three-phase or AC motors.

Sewage pumps transport sewage and untreated waste water (e.g. raw waste water). They are most commonly used in municipal waste water treatment plants but also in buildings and private homes (also see Sewage lifting unit), which cannot be connected to the municipal sewer due to the natural slope of the terrain. 

Types of sewage pumps

• Pumps for dry installation with single-vane impeller
  See Fig. 1 Sewage pump
• Submersible motor pumps (vertical installation) with single-vane impeller
  siehe See Fig. 2 Sewage pump
• Close-coupled pumps (ready-to-connect package systems)
  See Fig. 1 Sewage pump
• Torque flow pumps with free-flow impeller
  See Fig. 3 Sewage pump
• Pumps with diagonal impeller
  See Fig. 4 Sewage pump

The requirements for sewage lifting units are identical with those for waste water pumps. Clogging, for example, must also be prevented in sewage lifting units, even if solids contents are high. This is why they are fitted with special impellers such as single-vane or diagonal impellers.

The axial thrust is balanced by back vanes. Single or double mechanical seals are used as a shaft seal. Sewage lifting units are usually not self-priming.

To prevent wear sewage lifting units are designed with replaceable wear-resistant components (e.g. casing wear ring, wear plate, impeller wear ring), depending on the solids content (see Solids transport).

The shaft coupling is the connecting element between the electric motor and the pump hydraulic system. Slip-free shaft couplings employed in centrifugal pumps are divided into rigid and flexible shaft couplings.

Rigid shaft coupling 

Rigid shaft couplings are mainly used to connect perfectly aligned shafts. The slightest misalignment results in considerable extra stress on shaft couplings and adjoining shaft ends.

Examples of rigid shaft coupling types

• Sleeve coupling
• Muff coupling
• Serrated (splined) coupling
• Split muff coupling (DIN 115)
• Disc coupling
• Flange coupling
• Gear coupling

Flexible shaft coupling

Shaft couplings to DIN 740 are resilient (flexible), slip-free connecting elements fitted between driving and driven components, capable of partially compensating axial, radial and angular misalignment and shock loads.
See Fig. 1 Shaft coupling

Flexibility is usually achieved by the deformation of dampening, rubber or metal-elastic spring elements; their service life is heavily dependent on the extent to which misalignment has to be compensated. Different flexible shaft coupling designs are available.
See Fig. 2 Shaft coupling

If shaft misalignment occurs between the driver and the pump as a result of, for example, temperature fluctuations in the fluid handled (on heat transfer and hot water pumps) the double-cardanic coupling type design is often employed.
See Fig. 3 Shaft coupling

Gear couplings are flexible shaft connections for positive torque transmission and are particularly suited to compensating axial, radial and angular shaft offsets.

The design principle employed by curved-tooth gear couplings (see Curved-tooth gear coupling) prevents edge pressure when gears engage in the case of angular and radial offset, making these couplings almost wear-free.

The double-cardanic operating principle of curved-tooth gear couplings ensures that the reaction forces from angular and radial offsets are negligible and periodic fluctuations in the angular velocity do not occur.
See Fig. 4 Shaft coupling

A coupling with spacer sleeve (see Back pull-out design) allows the shaft seal and pump bearing assembly to be removed without removing the pump casing and the drive.
See Fig. 5 Shaft coupling

If precise data on the influence of the frequency of starts and the ambient temperature is not available, the load can be calculated on the basis of factors specified as reference values. No fixed value is laid down for the ratio of maximum torque to operating torque. This means that all coupling types can be taken into consideration according to their specific suitability. The calculation of the loading by torque shocks relates therefore to the maximum torque (see Starting torque). 

The calculation method for sizing flexible couplings given in DIN 740 only applies on the assumption that the coupling is the sole torsionally flexible element of a rotor, reducing the installation to a linear two-mass system. In all other cases it is necessary to carry out a vibration calculation.

Shaft efficiency is also known as pump efficiency.

The shaft protecting sleeve is fitted to the shaft and rotates in the bearing bush. It protects the pump shaft against mechanical damage caused by shaft seals and bearing shells (see Plain bearing) and against chemical damage caused by aggressive fluids (see Material selection). 

When designing the shaft protecting sleeve, care should be taken that any fluid handled that might penetrate the gap between the shaft protecting sleeve and the shaft cannot leak into the atmosphere. Sufficient axial space for expansion must be available and the shaft protecting sleeve (ideally at the impeller end) must be secured against tangential and axial displacements in relation to the shaft.

The shaft seal is a sealing element which seals the rotating shaft, of a centrifugal pump where it passes through the non-rotating pump casing reducing fluidleakage to atmosphere or the entry of air from outside to a certain level, and keeps wear of the sealing faces as low as possible.

Pumps are specially designed and manufactured to cater for a whole range of different applications. This process takes into account aspects such as resistance to the fluids handled, temperature and pump pressure. The appropriate seal type for the individual pumping requirements is chosen from a wide variety of different shaft seals.

The design is based on one of the two following principles: sealing by means of a narrow radial gap (parallel to the shaft axis) or a narrow axial gap (at a right angle to the shaft axis). For both sealing principles, the gaps may either employ a contact or non-contact design.
See Fig. 1 Shaft seal

If only non-contacting controlled gap seals are used, a considerable amount of leaking fluid can always be assumed. This sealing system is therefore less suitable for environmentally harmful fluids handled.

Shaft seals are by their nature susceptible to leakage, and with some types leakage is actually essential to ensure proper sealing functioning. The suggestion that a seal shaft provides "zero leakage" is therefore misleading. However, depending on the seal type chosen, the amount of leakage can vary considerably. A volute casing pump with a circumferential speed at the sealing area of 20 m/s and a pressure to be sealed of 15 bar which uses a gland packing for sealing has a leakage rate of about 5 – 8 l/h, while the leakage rate of a mechanical seal used under the same conditions is only approx. 6 cm³/h (0.006 l/h).

The leakage rate of 4 to 6000 l/h for a boiler feed pump sealed by a floating ring seal is particularly high; in this case, the diameter to be sealed is 200 mm and the pressure 40 bar, the rotational speed is 6000 rpm (~ 63 m/s).

Due to differences in pump designs the individual seal types are not necessarily suitable for every type of application. The type of seal to be employed depends on the sliding velocity, the pressure to be sealed and the fluid temperature.
See Fig. 2 Shaft seal

Contact-type shaft seal

In the case of contact-type dynamic shaft seals, the parts to be sealed move relative to each other. For this reason lip-contact and line-contact shaft seals (e.g. lip seals) are only suitable for use with very low pressure differences such as those occurring when sealing against bearing oil, and are usually not adjustable.
See Fig. 3 Shaft seal

Contact-type shaft seals can be classified as either static or dynamic. Dynamic seal types include gland packings and mechanical seals.
See Fig. 1 Shaft seal

Gland packing

The gland packing's application limit is primarily determined by the extent to which heat developing due to friction can be dissipated. For heavy-duty gland packings, leakage water is actually pre-cooled by means of an internally cooled shaft protecting sleeve and a cooling jacket.

The packing materials generally employed are braided cords made from asbestos-free yarn such as Ramie, Aramid, PTFE, graphite fibres or cotton, which are processed on special machines to form endless square braids.

The packings can be adjusted and are suitable for higher pressures and circumferential speeds than lip seals. Different packing variants are used depending on whether the pump is run in suction head or suction lift operation, or whether it handles clean or contaminated fluid.

In the case of positive pressure, the gland packing is equipped with three to five packing rings. These packing rings are pressed together axially via the gland follower. As a result they expand radially which means the pressure on the shaft protecting sleeve is increased. This has an influence on the clearance gap width and the leakage rate at this location.

The radial gap between the shaft protecting sleeve and the packing rings allows fluid to leak to the outside. This leakage is required to reliably dissipate the heat generated by friction from the gap. When tightening the gland bolts it is important to find a satisfactory compromise between an acceptable leakage rate and sufficient packing cooling.
See Fig. 4 Shaft seal

As the leakage with gland packings is relatively high compared with mechanical seals, the former are mostly employed for environmentally friendly fluids only.

The gland packing can be operated without cooling for fluid temperatures up to 120 °C.

When used with hot water up to 180 °C, the gland packing must be fitted with a cooling jacket. For higher temperatures cooling is ensured via a combination of an internally cooled shaft protecting sleeve and a cooling jacket.

If the pump is used in suction lift operation, a barrier fluid line and a lantern ring fitted after the first packing ring ensure that air cannot enter via the packing. Provided the pump handles a clean fluid, this barrier fluid is supplied via the pump's discharge nozzle or via an internal bore.
See Fig. 5 Shaft seal

As the pump discharge pressure is higher than the atmospheric pressure, air cannot penetrate the pump.

The barrier fluid pressure should normally be approx. 10 % or at least 2 bar higher than the highest pressure to be sealed.

A barrier fluid connection is also required under suction head conditions (positive pressure), if the fluid is contaminated. If this were not the case, the contaminants would be forced through the packing with the leaking fluid. The contaminants would settle at the contact face of the gland packing and rapidly destroy the shaft protecting sleeve due to their abrasive effect.

In this case, an external barrier fluid supply is the only suitable option. The lantern ring would then be fitted as the innermost ring.
See Fig. 6 Shaft seal

As the barrier fluid pressure is higher than the pump pressure, a certain amount of the barrier fluid mixes with the fluid handled inside the pump, so that compatibility between the barrier fluid and the fluid handled should be ensured.

When the gland packing is serviced, both the packing cord and shaft protecting sleeve must be assessed for wear. If the shaft protecting sleeve has a hard, wear-resistant surface, this generally has a positive effect on the gland packing’s service life. Chrome plating, surface nitriding or plasma coating are excellent methods for hardening shaft protecting sleeves at the area subject to packing ring abrasion. Surface hardness should be higher than 800-1000 HV (Vickers hardness).

This method is particularly important when the fluid's purity cannot be guaranteed at all times. As this hard coating is very thin, shaft protecting sleeves which have undergone such treatment cannot be remachined during servicing.

Mechanical seal

Unlike gland packings, mechanical seals have a sealing gap which is positioned at a right angle to the shaft axis. These shaft seal designs are also called axial or hydrodynamic mechanical seals. Compared with gland packings, they require less space and no maintenance.

Mechanical seals are well-suited for sealing low and high pressures and circumferential speeds. The risk of inappropriate operation is therefore very low.

However, considerable disadvantages arise through wear caused by abrasive fluids (see Abrasion). As is the case with gland packings, clean barrier or flushing fluids (e.g. cleaned by means of cyclone separators) help to keep abrasive particles away from vulnerable seal faces.

Pressed together by hydraulic and mechanical forces, two seal faces slide relative to each other during operation. The sealing gap lies between these precisely machined seal faces and is filled with a lubricating film, generally a liquid. The sealing gap width (i.e. the distance between both seal faces) is influenced by various factors, including the seal faces' surface quality (i.e. how rough or smooth they are) and the sliding velocity.

Leakage from mechanical seals is very low; the fluid leaks into the atmosphere in the form of vapour or droplets. To calculate the mechanical seal's leakage rate, a gap width of under 1 μm is normally assumed. Thanks to this extremely narrow gap, the leakage rate for mechanical seals is considerably lower than that for shaft seals with radial gaps.

A further important differentiating feature is that seals can be unbalanced and balanced. In the case of unbalanced mechanical seals, the seal face is exposed to the complete pressure to be sealed.

In the case of balanced seal types, a shoulder on the shaft or shaft sleeve ensures that only a portion of the fluid pressure is active as an axial force.

The load factor (k) characterises and defines the ratio of the hydraulically unbalanced area (A_H) and the seal face area (A).
See Fig. 7 Shaft seal

If the k value becomes smaller, the seal face loads are reduced. For this reason, only balanced mechanical seals are employed in high-pressure and high-velocity applications.

A low k value results in both an improved lubricating film and a higher leakage rate. However, an excessively low k value may in extreme cases cause the complete separation of the seal faces resulting in a loss of the sealing effect.

Alongside the hydraulic closing force, spring forces provide an additional axial force acting on the sealing gap. The springs can employ an open or enclosed design and be in contact with the fluid handled or not; they may or may not transmit torque.

Spring types employed

• Central spring, conical or cylindrical, mounted onto shaft as single spring
• Multi-spring arrangement consisting of concentrically arranged multiple springs
• Metal bellows
• Wave springs

The friction losses generated are lower than those of gland packings. Heat is generated in the shaft seal housing due to friction; depending on the amount produced, it can be dissipated either via convection from the seal housing to the atmosphere or via forced circulation through an externally installed heat exchanger.

As with gland packings, mechanical seals are available in various designs and configurations to handle diverse operating conditions.

Frequently used designs

• Single, unbalanced mechanical seal as a typical example for a centrally arranged, conical single spring: The variant shown here is for "dead end" installation, i.e. there is no additional fluid circulation in the mechanical seal area.
  See Fig. 8 Shaft seal
• Unbalanced mechanical seals are used for pressures of up to max. 15 bar and sliding velocities of up to max. 15 m/s. In general, a sufficient proportion of friction heat generated in the sealing gap can be transferred to the fluid handled and dissipated from the shaft seal housing to the atmosphere via convection. If the fluid handled is cold, the friction heat is absorbed by the fluid itself. One variant is the rubber bellows seal (bellows-type mechanical seal).
  See Fig. 9 Shaft seal
• Unbalanced mechanical seal with stationary spring assembly: this design is used for higher sliding velocities and ensures the springs can reliably fulfil their task (rotary spring assembly would entail a risk of broken springs due to high centrifugal forces).
  See Fig. 10 Shaft seal

Varying spring arrangements are just one example of the distinctive features represented in the wide range of mechanical seal designs tailored for various operating conditions.

Mechanical seal arrangements

• Single seal arrangement
  See Figs. 8, 9 and 10 Shaft seal
• Multiple seal arrangement
  See Fig. 11 Shaft seal

In the case of "back-to-back" arrangements, a barrier fluid is fed into the space between the two mechanical seals. Its pressure should be approx. 10 %, and at least 2-3 bar, higher than the pressure of the fluid handled by the pump.
See Fig. 11 Shaft seal

This barrier fluid ensures that the fluid handled does not leak into the atmosphere. Before considering this arrangement, it should be established whether a zero-leakage pump such as a canned motor or mag-drive pump would be more suitable for the application.

As the barrier fluid absorbs the friction heat generated by the two mechanical seals, it must be circulated, i.e. removed from the seal cavity, cooled and returned to the seals.

The barrier fluid pressure is generated by a barrier fluid system (thermosyphon vessel) or pressure booster. In the case of tandem seals, the space between the seals is flushed by unpressurised quench liquid (quench). If the leaking fluid handled by the pump has a tendency to crystallise when in contact with air, a seal arrangement comprising two rubber bellows seals should be used. It is important that the quench liquid and fluid handled are compatible.
See Fig. 12 Shaft seal

Instead of using an outboard mechanical seal, it is also possible to install a simple sealing element such as a lip seal or packing ring. It is fitted as a back-up seal for the main seal to prevent leakage (e.g. in the case of hazardous fluids) and to safely and reliably dissipate heat.

Tandem seals are employed when a high internal pump pressure requires distribution to two mechanical seals. The barrier fluid pressure level then lies between the pressure to be sealed and the atmospheric pressure. The pressure handled by the inboard seal corresponds to the difference between the pressure to be sealed and the barrier fluid pressure; the pressure handled by the outboard seal corresponds to the difference between the barrier fluid pressure and the atmospheric pressure. The barrier fluid must circulate in order to dissipate the friction heat generated by the seals.
See Fig. 13 Shaft seal

These mechanical seal types are used in the boiling or pressurised water reactors of nuclear power stations and are installed in main coolant pumps to seal extremely high pressures.

A three-stage seal arrangement is employed to seal a pressure of 160 bar in a pressurised water reactor, for example.

The pressure must be distributed via an auxiliary system, e.g. a three-stage cascading system of throttles arranged in the seals' bypass lines. A defined amount of water flows via the bypass line. Pressure is thus reduced by approx. 33 % at each throttle. The reduced pressure at each stage's output is the operating pressure for the next stage's input. This throttling and recirculation of the barrier fluid ensures the pressure is reduced and the friction heat removed from the sealing stages.

In the case of boiler feed pumps, seals have to cope with high sliding velocities, heat transfer from the fluid handled and the heat generated by friction.
See Fig. 14 Shaft seal

The sealing gap temperature is generally higher than the fluid temperature in the seal housing. The latter can be kept well below 100 °C by circulating the fluid through to an external cooler by means of suitable pumping devices inside the pump. Pumping screws, holes in the shaft protecting sleeve or small pumping discs serve as pumping devices.
See Fig. 15 Shaft seal

Magnetic filters ensure that the circulated water is absolutely clean. With high-specific speed pumps,a venting tank is essential to reliably remove any air from the circulation liquid.

Detrimental dry running of the mechanical seal may occur if the pump is operated without liquid fill and in the event of a major ingress of gas, a high gas content or the evaporation of the fluid handled. Due to its low density, the gas always tends to move to smaller diameters which is the sealing gap of seals in most cases. The presence of air in this space leads to dry running and also impedes sufficient heat dissipation from the sealing gap resulting in thermal overload of the seal faces and mechanical seal failure (heat stress cracks) within a very short time.

External cooling circuits are not used if the heat losses generated by the seal can be dissipated to the atmosphere via free convection and heat radiation.
See Fig. 16 Shaft seal

Other forms of cooling comprise a fan impeller mounted to the pump shaft to intensify convection (forced convection). In both cases the seal housing is provided with fins, at a right angle to the shaft axis (without fan impeller) see Fig. 16 Shaft Seal, and parallel to the shaft axis (with fan impeller).
See Fig. 17 Shaft seal

In the case of uncooled mechanical seals operated at high temperatures, the temperature in the sealing gap is generally higher than the temperatures in the sealing gaps described so far. This means that the boundary between the liquid and vapour phase in the sealing gap inevitably shifts towards the sealing gap inlet, increasing the risk of insufficient lubrication.

Non-contact seal with radial gap

This category encompasses all throttling gaps with or without labyrinths, pumping rings/screws and floating ring seals.

The sealing gap width between the stationary component and the rotating component is designed to be as narrow as possible in order to minimise leakage. However, it is important to ensure that the parts do no rub against each other. Leakage on a rotating shaft is slightly lower than during standstill.

The fluid flowing through the gap allows the pressure to be reduced in relation to the atmospheric pressure. On throttling gaps and floating ring seals this is achieved in the gap due to fluid friction and due to flow losses when the fluid enters or leaves the gap.

Floating ring seal

• The major advantage of floating ring seals is the fact that the components are not in contact. However, the time and costs required to provide the barrier condensate, its treatment and relevant control equipment are substantial.
• Thanks to their non-contact nature, these seals can be used for high circumferential speeds and mid-level pressures (30 to 50 bar).
  See Fig. 18 Shaft seal

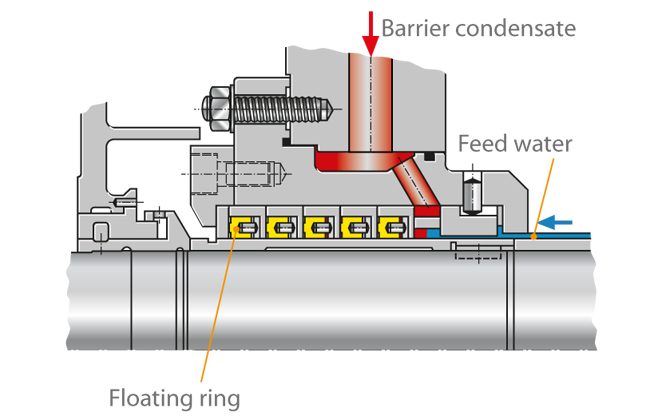
• With regard to their reliability, they are almost independent of the feed water's chemical composition.
• The floating ring seal consists of several short throttling rings fitted in succession which can move in a radial direction and centre themselves automatically due to the pressure distribution on the ring. A cold barrier condensate injected into the seal ensures that hot water from the pump does not escape to the atmosphere (controlled system). As long as the pump is in operation or under pressure, barrier water supply must be ensured.
• The floating ring seal is occasionally employed in boiler feed pumps. Its barrier condensate quantity can be controlled via the barrier condensate's pressure and temperature difference.
  See Fig. 19 Shaft seal​​​​​​​

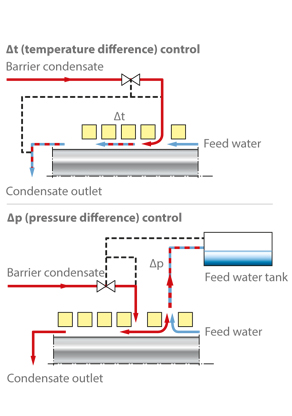
• For differential temperature control
• (Δt control), the difference between the temperature of the barrier condensate at the outlet and that of the injection condensate is defined. In the case of boiler feed pumps, the amount of feed water escaping from the inside of the pump is very low, while penetration of cold water into the pump can be ruled out.
• For differential pressure control (Δp control), the difference between the injection pressure and the inlet pressure is defined. A very small amount of barrier condensate flows into the pump. This puts high demands on the cleanliness and gas-free condition of the barrier condensate required to prevent the main circuit from being contaminated.

Instead of a floating ring seal, a labyrinth seal can also be used.

Labyrinth seal

• The labyrinth seal is a firm throttling bush with a circular groove profile. As radial movement is impossible with this type of seal, the diametral clearance must be wider than that employed with floating ring types. As a consequence, the leakage rate is higher, in turn requiring a higher barrier water flow rate.

Centrifugal seal

• This type of shaft seal generates pressure itself in order to counteract the differential pressure to be sealed; it is frequently backed up by a standstill seal. Designed as spring-loaded mechanical seal, it is opened by centrifugal forces at very low speeds and thus protected against wear. See Fig. 20 Shaft seal

• The actual centrifugal seal (fitted as an auxiliary impeller using a liquid ring at the outer diameter) operates contact- and wear-free.

Pumping ring/screw

• Optimally designed pumping rings/screws (thread pitch of the stationary part directed against the pitch of the rotating part) can also generate a back pressure capable of balancing the pump's internal pressure when the pump is running. The pressure balance achieved this way depends on the rotational speed, thread length, gap width and mean gap diameter.
• Heads of 10 to 30 m can be achieved.
• As soon as the shaft stands still, however, the pumping ring/screw has only a throttling effect comparable with a labyrinth gap.
• If a pumping ring/screw is to serve as a pump seal, it needs to be backed up by a contact-type standstill seal.
  See Fig. 21 Shaft seal​​​​​​​

Hydrostatic seal

• Due its design, proper functioning of the hydrostatic seal as a non-contact seal is only ensured at pressures from 20 bar. The pump drive must not be started until this pressure level is reached.
• As the seal is very sensitive to solid particles, the barrier water which feeds the seal must be extremely clean.
• The sealing gap is self-adjusting. Depending on gap geometry and the pressure to be sealed, the sealing gap will adjust itself at about 10 μm.
• The gap's stiffness is very high at full operating pressure (160 bar). To move the gap from its balanced position by 1 μm, an external force of approx. 4000 N would be necessary.
• The gap with which the seal operates may be very narrow, but it is finite, and as such exhibits a considerable leakage rate (p = 160 bar, n = 1.500 rpm; sealing diameter at 260 mm, Q = 800 l/h). It is therefore necessary to back up the hydrostatic seal with a low-pressure seal that provides sealing to atmosphere.
  See Fig. 22 Shaft seal​​​​​​​

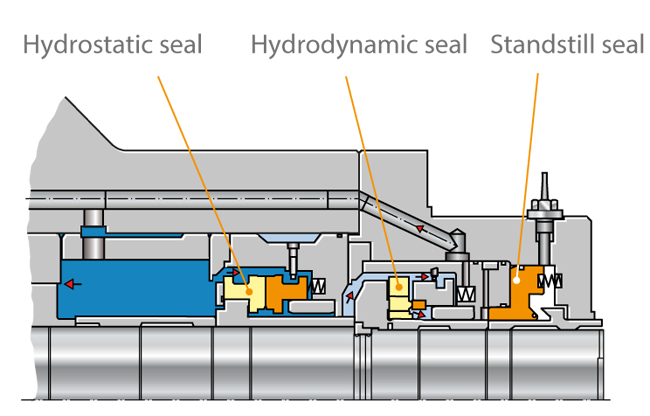
• Due to the hydrostatic seals’ operating limitation at low pressures, they have been replaced with hydrodynamic mechanical seals in many nuclear power stations.
• They are only used in main coolant pumps of pressurised water reactors.

Static contact seal

Static contact seals include O-rings. These are moulded seals and are defined as "rings with circular cross section made of elastic materials; they seal through the effect of slight bracing during installation, intensified by the operating pressure" according to DIN 3750. Their symmetrical cross-section rules out incorrect installation.

As connecting components can be easily calculated and designed, their use is widespread.

O-rings are employed on all the shaft seals described here. However, they can only be used as static sealing elements or to seal areas where slight axial movement is occasionally required.

They are manufactured at different hardness degrees, specified as shore hardness (A or D). The hardness scale ranges from 0 to 100, 0 being the lowest and 100 the highest hardness unit.

The majority of O-rings used on mechanical seals are elastomer rings with a shore A hardness of 70 to 90. These O-rings are used for sealing between the shaft sleeves and the shaft, and between the primary ring or the mating ring and the respective components they are connected with. They ensure that the spring-loaded seal component can follow small axial shaft movements.

Their significance is often underestimated: ultimately, each shaft seal is only as good as its O-ring. O-rings must be matched to the fluid handled, cover a defined temperature range and provide good ageing resistance. Moreover, it is important to use a high-quality O-ring grease which meets the operating requirements. Besides providing long-term lubrication, the grease must be compatible with the fluid handled and must not attack the O-ring.

Elastomers which swell less than 10 % in the operating fluid and do not chemically react with the fluid handled are suitable for use as a mechanical seal's secondary seal. A number of elastomers are available for this purpose which react differently in a reference oil with regard to temperature resistance or swelling properties.
See Fig. 23 Shaft seal

Particularly critical are applications in chemical plants and refineries where pumps are frequently employed to handle different types of fluids.

The shaft seal ring, often also called radial shaft seal ring or lip seal, is a contact-type shaft seal. In most cases it cannot be adjusted and is only suited for use with very low differential pressures.

Shear stress (τ) on fluid particles of a fluid of normal viscosity (see Viscosity) and on walls in contact with the fluid occurs in the form of a tangential force per unit of area when particles are displaced in opposing directions or when fluid moves along a wall. This force is opposed to the direction of fluid movement. In accordance with Newton's law of viscous shear, τ is the product of dynamic viscosity and the velocity gradient (see Viscosity).

Ein abgeschirmtes Kabel besteht aus einem Leiter, der mindestens von einem Kabelschirm (leitfähige Hülle) umschlossen ist. Dieser Kabelschirm dient dem Schutz (Abschirmung) des im Inneren verlegten Leiters gegen elektromagnetische Einflüsse von außen.

Shielding refers to the protection of a conductor from external electromagnetic influences (also see Shielded cable).

If the angle of attack of a vane cascade differs from the inlet angle of the vanes (see Shock-free entry), the loss resulting from the forced change in velocity is called shock loss or impact loss.

It occurs when the flow rate (Q) of a pump is smaller or larger than the value resulting in a shock-free approach flow (Q_shock-free) for the respective vane geometry. A change in the flow rate entails a change in the inflow angle and therefore the incidence angle of the vanes.

A meridian velocity (c_m.0) upstream of the cascade (subscript 0) can be calculated for a given flow rate (Q). The circumferential speed at the impeller inlet (subscript 1) in the flow area is assumed to be u₁. Therefore, in the case of a vortex-free approach flow (i.e. c₀ = c_{m. 0}), the flow approaches the vane with a relative velocity (w₀). It is also assumed that the resulting relative inflow angle is β₀ and the vane angle at the impeller inlet is β₁. If the flow rate does not equal the flow rate at shock-free entry (Q_shock-free), as characterised by the condition β₀ = β₁, the flow must be abruptly diverted after entering the vane cascade, i.e. from the inflow angle β₀ to the angle β₁ so that it is able to follow the direction of the vanes.

The meridian velocity in this case remains unchanged (c_m.1 = c_m.0) (the blocking effect caused by the vanes' thickness shall be ignored). This case is shown in Fig. 1 for an operating point at overload with Q > Q_shock-free. See Fig. 1 Shock loss

The shock component (w_shock.imp) causes a calculated head loss of:

ζ_shock.imp     Shock coefficient for the impeller vane

g                Acceleration due to gravity

An analogous analysis can be used when evaluating the shock losses in the diffuser. It must be taken into account that, in contrast to the case of vortex-free flow to the impeller inlet, the direction of absolute flow is not independent of the flow rate.

In a first approximation, it can be assumed that the direction of the relative flow (w_2.imp) leaving the impeller remains constant within the range 0.75 ∙ Q_opt ≤ Q ≤ 1.25 ∙ Q_opt.
See Figs. 2, 3 Shock loss

When calculating the shock losses, it should be taken into account that the shock coefficient in the low flow range is greater than in the overload range (see Operating behaviour).

This can be explained by the fact that separation occurs under low flow conditions as a result of shock approach flow, particularly in the outer region of the vane cascade, and this separation ultimately results in suction recirculation of the fluid when the shock approach flow becomes extreme.

In a vane cascade, shock-free entry is given if the relative flow (see Relative velocity) of the fluid entering the impeller or the absolute flow upstream of the diffuser, hits the vanes (in the same direction as the median line of the vane profile).
See Fig. 1 Vane cascade

Shock-free entry is usually given at the design point, but in certain special cases impellers, such as inducers are designed for non-shock-free entry. Non-shock-free-entry which normally occurs during low flow or overload operation (see Operating behaviour) causes so-called shock loss.

Shut-off elements are pipe components which coordinate flow. This can mean controlling flow volume incrementally (globe valve) or switching between fully closed/fully open positions (ball or plug valve) (also see Valve).

The shut-off head of a pump indicates the amount of pressure required to reach a condition where the flow rate in a vertical pipe connected to the operating pump becomes zero.

The term SI is the abbreviation for "Système international d’unités", which is the international system of units. This system defines a number of base units that can be combined to create further units.

In the context of mechanical and hydrodynamic quantities, the base units are m for length, s for time and kg for mass.

The SI system is based on the International System of Quantities (ISQ), was introduced as long ago as 1960 and is now the world's most widely used system of units for physical quantities.

Side channel pumps share the characteristics of both positive displacement pumps and centrifugal pumps. In side channel pumps the power of a star-shaped impeller (e.g. star impeller) rotating concentrically in a casing is transferred to the fluid handled in a side channel arranged next to the impeller.

The star impeller is very simple in design. It has straight radial vanes and no impeller shrouds. Instead, the casing walls surround its circumference and its sides. Narrow clearance gaps are provided between impeller and casing. The casing is designed with a side channel on one side or with a side channel each on both sides. The side channel, which leads around the entire circumference, is interrupted in one point (between the inlet and the outlet slit). See Fig. 1 Side channel pump

When the impeller rotates, the fluid moves to and for several times between the cells of the star impeller and the side channel, which causes a strong transfer of energy by means of momentum exchange between the fluid rotating at almost the same high circumferential speed as the impeller and the fluid flowing slowly in the side channel.

This momentum exchange occurs repeatedly at the circumference and generates a very high head, which is 5 to 15 times as high as the heads generated by radial impellers of the same size rotating at the same circumferential speed.

Apart from high heads, which can be multiplied several times in case of multistage side channel pumps (see Multistage pumps), side channel pumps also have the advantage of being self-priming (see Self-priming pump). 

Similar to the principle of water ring pumps the water remaining in the pump casing forms a water ring with a free surface when the star impeller rotates and air is sucked into the side channel pump through the pump suction nozzle.

This water ring would rotate concentrically and ineffectively in the casing if the side channel were not interrupted in one point of the circumference. The displacement action decreases the inner radius of the water ring in this part of the circumference. This also reduces the air-filled pockets between the radial vanes of the impeller. The side channel pump now operates as a compressor based on the principle of positive displacement, like a water ring pump.

Side channel pumps are used for applications which benefit from their self-priming capability and their high heads at low flow rates (compared to normal centrifugal pumps of the same dimensions). The only pumps exceeding the heads of side channel pumps are peripheral pumps.

Side channel pumps with a drive rating of more than 4 kW are rare because of their relatively low pump efficiency.

The similarity theory requires that three essential conditions be met for hydraulic model tests: geometric (length), kinematic (velocity) and dynamic (forces) similarity between the model (M) and the full-scale version (G). Kinematic and dynamic similarity are grouped together under the heading of physical similarity (see Affinity laws).

Geometric similarity

In order to fulfil the condition of geometric similarity, all the linear dimensions of the model pumps (I_M) and the corresponding dimensions of the full-scale version ("prototype") (I_G) must have the same ratio (m_I; model scale):

The geometrically similar reproduction of a pump and its system environment in model form is only required for sections relevant for the actual flow analysis. Establishing geometric similarity on the discharge side of the system is irrelevant if the fluid flow analysis is confined to the pump's suction side.

The full-scale version's wall surface roughness can only be reproduced in the model with limited accuracy, which is insufficient to achieve a microscopic level of geometric similarity, meaning that the boundary layer flow and the resultant  pressure losses arising due to wall friction can only be examined to a limited extent.

Kinematic similarity

Kinematic similarity requires the proportionality of the corresponding velocity vectors in the model (v_M) and the full-scale version (v_G) (see Velocity triangle). The requirement of a constant velocity scale can strictly speaking only be fulfilled in conjunction with geometric and dynamic similarity:

Any deviation from geometric similarity will result in a roughly equal deviation from kinematic similarity. In model tests, deviations from kinematic similarity often manifest themselves via discrepancies between the degree of turbulence in the model flow and the flow in the full-scale version. This degree of turbulence has an influence on the change from laminar to turbulent flow (see Boundary layer, Fluid mechanics), on the possible occurrence of flow separation, and therefore on flow losses. Often, these cannot be assessed with sufficient accuracy on a model.

Experience has shown that the different types and structures of the boundary layers in the model and the full-scale version result in only minor deviations from kinematic similarity provided that there are no significant differences in flow separation zones and investigations are not concerned with areas close to surfaces such as those of vanes.

Dynamic similarity

In order to fulfil the requirement of dynamic similarity, a defined scale ratio (m_f) must apply to all forces (F) which determine flow phenomena in both the model (M) and the full-scale version (G).

Apart from the two-phase effects in two-phase flow, the forces of significance in hydraulic pump modelling are inertia, gravity, pressure and friction.

Dynamic similarity with regard to the inertia and gravity forces in a model and full-scale version is expressed by the fact that the Froude number (Fr) is constant:

v   Characteristic flow velocity
l    Characteristic length
g   Local acceleration due to gravity

The same applies to the Reynolds number (Re):

Re_M = Re_G

v    Kinematic viscosity of the fluid handled

Dynamic similarity with regard to the pressure and inertia forces present in the model and the full-scale version is expressed by the same values of the  Euler number (Eu):

Eu_M = Eu_G

P    Characteristic pressure (pressure difference)
ρ    Fluid density
g    Local acceleration due to gravity

In the case of centrifugal pumps, the Euler number expresses the relationship between the pressure rise in the pump (i.e. the characteristic pressure difference) and the circumferential velocity at the impeller outer diameter (u₂) (i.e. the characteristic velocity) and is as such termed the head coefficient. Achieving the same Euler number or head coefficients in both the model and the full-scale version requires that both geometric and kinematic similarity are ensured and that the same Froude and Reynolds numbers are present in both the model and the full-scale version.

When transient flows with a frequency f are involved, the Strouhal number comes into play. In hydraulic modelling, a frequent deviation from dynamic similarity arises from the fact that the Froude or Reynolds numbers in the model and in the full-scale version are not the same due to technical reasons relating to the tests. Many years of experience have enabled certain ranges of these numbers to be obtained in the model and the full-scale version without substantially impairing physical similarity (see Efficiency scale-up).

Single-phase alternating current, is alternating current, that flows through a two-core cable and is related to three-phase current.

The single-phase asynchronous motor is an electric motor that is operated using single-phase current.

The rotor winding is of is a squirrel-cage type and the stator winding comprises a main and an auxiliary winding whose magnetic axes are electrically offset by one half of a pole pitch (90°). The auxiliary winding is used to generate a rotary field component in the air gap of the machine so that the machine can self-start.

For this purpose, the motor is briefly connected to the power supply via a resistor or start capacitor at start-up. If a run capacitor is used, it also remains on during operation.

All single-phase asynchronous motors have a typical shunt characteristic (i.e. rotational speed gradually decreases as load increases) due to the constant air-gap flux.

Single-vane impellers can be classified in radial, open diagonal and closed single-vane impellers.

Siphoning lines are used to safely draw liquids from storage tanks from the top. In addition, they allow the safe siphoning of liquid and the reliable venting of the suction line at the end of operation or in the event of a malfunction.

Siphoning lines are used in groundwater pumping stations to transport water from individual wells into a collecting well from which it is then pumped into a reservoir by self-priming pumps. The difference in levels (e) represents a gradient which generates the flow velocity (v) required to overcome the head loss (Σζ∙v²∙(2∙g)^-1) i.e. the resistance coefficient (ζ) and the acceleration due to gravity (g).

See Fig. 1 Siphoning line

The siphon flow rate (Q) is calculated using the following equation:

v      Flow velocity in m/s

Σ ζ   Sum of resistance coefficients of pipe sections, elbows, etc. (see Pressure loss)
d      Inside diameter of piping in m
e      Height difference between the two water levels in m
Q     Siphon flow rate in m³/h

The siphoning line can only operate if the absolute pressure (p_S) at the apex of the system exceeds the vapour pressure (p_D) as determined by the water temperature. This condition is satisfied if

or, if the apex lies close to the collecting well.

e_s         Height difference between apex and inlet side water level in m
Σζ_e,s    Sum of resistance coefficients from the inlet to the apex of the system
S         Safety margin of 1 to 2 m (depending on quality of
           pipeline construction)
p_D        Vapour pressure in bar
p_b        Atmospheric pressure in bar

Dissolved gases (see Gas separation) are continuously released out of solution at the apex of the pipe and have to be removed.

Often submersible borehole pumps which pump the water directly into the reservoir are used instead of siphoning lines. See Fig. 1 Domestic water supply system

The slave is a participant in a communications system, that can only participate in the exchange of data by way of the master.

Slip plays an important role in calculating the radial or mixed flow impeller of a centrifugal pump, with which a specific head (H) is to be generated for the flow rate (Q). If the vanes of the impeller were infinite in number (∞) and infinitely thin, pump power output (P_th.∞) would be theoretically (th) calculated as follows in the presence of an ideal (friction-free) liquid:

An ideal fluid and infinite number of vanes lead to a vane-congruent flow, i.e. a flow that follows the vane contours in the impeller, and yield the theoretical head (H_th.∞) as per EULER's fundamental equation (see Fluid mechanics). A finite number of vanes (z), however, leads to a deviation in the flow direction of the impeller from the vane contours. The mean angle of the relative velocity at the impeller outlet in particular is smaller than the vane outlet angle for a finite number of vanes (z). This deviation, which increases as the number of vanes (z) decreases, means that the theoretical head (H_th), and thus the theoretical pump power output (P_th) (for identical flow rate and density), are smaller if the number of vanes is not infinite:

The result is a difference in power for the slip (ΔP_th.) which equals approximately 25 to 60 percent of pump power output for conventional radial impellers. Slip can be expressed mathematically as follows:

Slip is not synonymous with a loss in power, since it is based on the assumption of a friction-free fluid flow at the impeller.

The ratio of H_th.∞ to H_th is expressed by the slip factor (1 + p), which empirically references the influence of the number of vanes, impeller geometry, impeller diameter, vane angle at the outlet, and diffuser element behind the impeller.

The correlation between heads H and H_th is determined by the hydraulic efficiency (η_h).

Calculating an impeller based on the slip theory requires a great deal of experience and primarily involves numerical arithmetic techniques (see CFD). Axial impellers are calculated based on the aerofoil theory, which also utilises numerical flow calculation methods.

The slip ring rotor characterises an asynchronous motor whose rotor has a slip ring design. Unlike squirrel-cage rotors, slip ring rotors use rotor phase windings that are short-circuited via slip rings at defined intervals (also see asynchronous motor).

The sludge pump is a type of pulp pump.

A slurry pump is also known as a lined pump or dredge pump and is a centrifugal pump for transporting a fluid handled containing highly abrasive solids (see Abrasion) such as flotations, suspensions of slag, coal or ore in mining and sinter sludges, or in sand and gravel extraction. They are particularly heavily exposed to erosive wear (see Erosion). They are therefore designed in such a way that their wetted surfaces are hard-faced by deposit welding and the components exposed to wear such as rings, bushes, discs, casing inserts, impellers and all types of linings, can easily be replaced by new ones. They must therefore be reasonably inexpensive and consist of materials which are particularly resistant to abrasion or a combination of abrasion and corrosion. See Fig. 1 Slurry pump

The operating requirements also include quick and easy pump dismantling and a reliable spare parts service for the replaceable parts. In addition to these pumps specifically developed for hydraulic solids transport, there is a number of centrifugal pumps that are, depending on their design and material properties, suitable for handling fluids of different contamination degrees and solids content (see Waste water pump and Sewage pump).

The term smooth running of centrifugal pumps as viewed from a technical perspective refers to the evaluation of mechanical vibrations generated by a pump.

DIN ISO 10816 for the "Evaluation of machine vibration by measurements on non-rotating parts" assesses vibration class as a function of vibration velocity for three machine groups used in centrifugal pump applications.

ISO 7919 provides general guidelines about how to measure and evaluate machine vibrations if measurements are performed directly on rotating shafts. In this way, shaft vibrations can be determined with a view to changes in vibration behaviour, such as unusually high dynamic loads, or monitoring of radial play.

The vibration displacement amplitudes ascertained in this context correspond to the recommended limit values as a function of rotational speed.

The vibration velocity and amplitude are measured both on the rotating pump shaft and at various locations on the pump casing and foundation, as agreed between the customer and contractor, using electrodynamic vibration acceleration, vibration velocity, and vibration displacement sensors. Pump shaft measurements must be performed in the direction of the pump shaft and in several defined directions normal to the pump shaft.

The smooth-running characteristics of the drive, the tuning of the pump foundation, the vibration behaviour of the piping connected to the pump, and ambient noise (including from surrounding persons) should also be factored into the evaluation.

A centrifugal pump exhibits satisfactory smooth-running characteristics when its balanced rotating internals (see Unbalance) enable a rotationally-symmetric flow. This is typically the case at optimal flow rate (Q_opt) and with turbulence-free inflow (see inlet conditions) if the NPSH available is sufficient. If the NPSH available is insufficient, cavitation occurs in the impellers that is frequently not rotationally symmetric and can thus lead to transverse forces of varying intensity (see Radial thrust). Operation in a significantly low-flow range is definitely possible for centrifugal pumps with radial impellers but should be avoided or at least minimised for larger pump units.

Mixed-flow centrifugal pumps and axial flow pumps in particular cannot be operated freely in the low-flow range (e. g. propeller pumps with Q_min/Q_opt ≈ 0,8). When the flow breakaway limit is reached, flow breaks away from the impeller vanes in an irregular pulsating pattern and the pump no longer runs smoothly due to the eccentric effect caused by the resulting force. This limit, which is generally very pronounced for propeller pumps, can be counteracted by impeller blade pitch control so as to reduce the incidence angles and the flow rates. The Q_opt value then declines, however, and the Q_min/Q_opt ratio of approximately 0.8 is reinstated.

Measures for correcting rough running

• Rectify any unbalance.
• Optimise inlet conditions.
• Avoid unnecessary elbows upstream of the pump.
• Install devices that straighten flow, minimise turbulence, and equalise conditions in the suction line.
• Increase the NPSH available by selecting sufficiently sized piping diameters and fitting low-loss valves, elbows, and other fittings to achieve a low-loss flow upstream of the pump.
• Reduce the NPSH required by the pump by using an inducer, enlarging the suction eye of the impeller, specially shaping the vanes, and introducing a light co-swirl effect (see Vortex flow)) 
• Avoid low-flow operation through closed-loop control measures such as adjusting the impeller blade pitch and bypassing or by using additional, smaller pumps (half-load pumps).

The soft start throttle is an economical and robust control gear of simple design for squirrel-cage motors with low power ratings. It is used to control starting current, starting torque and the level of soft start control required (also see Starting method).

The soft starter is an electronic solution for gradually accelerating and decelerating or braking components (e.g. asynchronous motor) when they are started and stopped (also see Starting method).

The soft starting process encompasses all measures (e.g. use of a soft starter), that enable gradual acceleration and deceleration or braking of components (e.g. asynchronous motor) when they are started and stopped (also see Starting method).

Solar pumps are normally used for handling water in sunny regions without a mains supply. The power required to drive the pumps is generated by a photovoltaic system. Their main applications include the provision of water for cattle troughs and irrigation, and drinking water supply (see Photovoltaic pump system).

Fluids can be used for the transportation of fine- and coarse-grained solids. This process requires the use of piping.

It must be taken into consideration that, in contrast to clear liquids, such mixtures (sludges, pulps, suspensions) tend to separate under the influence of gravity or centrifugal forces. Coarse grain sizes and significant differences in density between the solid and the carrier liquid will encourage separation. Its extent can be gauged by the settling velocity of a solid particle in the still liquid. Turbulence (see Fluid mechanics) in the flow through the pipeline and, due to asymmetrical flow, pressure differences on the solid particles in the vicinity of the pipe wall (see Boundary layer) will tend to counteract this separation process. For this reason the flow velocity as well as the grain size and the solids content in the liquid (i.e. the concentration) will determine the nature of the solids transport.

Solids transport examples 

• Sludge transport (homogenous mixture of very small particles of high concentration)
• Suspended particle transport (homogenous mixture of low concentration)
• Jumping particle transport (non-homogenous mixture, with higher concentration at the bottom of horizontal pipes)
• Strand-type particle transport (first sediment layers in the case of horizontal pipes, and concentration at the centre of vertical pipes)
• Slug-type particle transport (transient conditions)

If the permissible concentrations are exceeded, or if the minimum velocities cannot be attained, there is a risk of pipe clogging. These phenomena play a less significant role where the transportation of pulp suspensions (see Pulp pumping) is concerned.

Mixtures of solids and liquids can also be pumped. Considerations regarding wear and economic efficiency determine which pump type is most suitable for this application. Piston pumps are, for instance, employed for handling fine grained materials (grain size up to 3 mm) provided that the periodic pressure fluctuations associated with this type of pump do not rule out its use (see Positive displacement pump).

In the case of coarser grain sizes (see Erosion) the pumps used are exposed to a greater or lesser degree of wear via contact with solids. Employing specialised pump types such as slurry pumps or using appropriate pump materials (see Materials, Plain bearings) can retard the wear process, making application economically viable.

In extreme cases it is necessary to resort to feeding systems designed in such a way that the high-pressure pump handles clear liquids only, while the solids are fed into the pump discharge line (see Pump system) via sluices or tubular chamber feeders.

The pressure loss associated with flowing mixtures of solids and liquids in pipelines is calculated using the same equations as those used for clear liquids. In this case, the pipe friction coefficient (λ) also takes into account the additional frictional losses arising from the solid particles making contact with each other and the pipe walls. The pressure losses can be plotted as a function of the flow rate (Q); this method can also be used to determine any given concentration (c_T). See Fig. 1 Solids transport

The pump's differential pressure Δp_p = f(c_T) may also rise with increasing concentration of high-density solids.
The minimum value of these resistance curves also determines the minimum flow velocity which must be maintained in order to prevent clogging (see Operating point).

Sound insulation is a passive form of noise abatement whereby the pump and drive are enclosed in special sound insulating or sound absorbing wall elements (also see Noise in pumps and systems).

The term sound level can refer to loudness as it is perceived by humans or to the sound pressure level as a measurable amplitude of sound (also see Noise in pumps and systems).

The sound pressure level is a measure for describing the intensity of sound. Its unit is the db (decibel).

The specific energy (Y) is the useful mechanical energy transmitted by the centrifugal pump to the fluid handled, per unit mass of fluid handled. It is expressed using the SI units Nm/kg or m²/s².

The relationship between the head (H) and the specific energy (Y) is as follows:

Y = g · H

g    Acceleration due to gravity

Figure 1 shows the specific energy Y lines across a pump system.
See Fig. 1 Specific energy

The specific speed (n_s) is a characteristic coefficient derived from the similarity conditions which allows a comparison of impellers of various pump sizes even when their operating data differ (flow rate and head at best efficiency point, rotational speed). The specific speed can be used to classify the optimum impeller design and the corresponding pump characteristic curves.

See Fig. 1 Specific speed

Defined as the theoretical rotational speed at which a geometrically similar impeller would run if it were of such a size as to produce 1 m of head (H_opt) at a flow rate (Q_opt m³/s at the best efficiency point, the specific speed is expressed in the same units as the rotational speed:

Q_opt in m³/s     Flow rate at η_max
H_opt in m         Head at η_max
n in rpm          Pump speed
n_s in rpm        Specific speed

A dimensionless characteristic coefficient in accordance with DIN 24260 can be established using the following equation:

n_s* in rpm^-1      Rotational speed
Q_opt in m³/s      Flow rate at η_max
H_opt in m           Head at η_max
g = 9.81 m/s²   Acceleration due to gravity

The following relationship exists between the numerical values of the dimensional and dimensionless coefficients:

The values to be inserted in the above equation are the optimum head Hopt for one stage in the case of multistage pumps, and the optimum flow rate Q_opt for one impeller half in the case of double-entry impellers.

The fluid flow through the impeller changes with increasing specific speed, i.e. radial impellers have low specific speeds, mixed flow ("diagonal") impellers have a higher specific speed range and axial impellers have the highest specific speeds. Establishing the specific speed n_s via a graph:
See Annex, Specific speed, Fig 2

Diffuser elements on radial casings such as volute casings are also required to become larger and larger with increasing specific speed as long as the flow can be guided through the impeller in a radial direction. Eventually (i.e. at high specific speeds) the flow can only exit axially, e.g. via tubular casings.

The specific speed's numerical value is also needed to select the influencing factors required for the conversion of pump characteristic curves, for example, if fluids of higher viscosity or solids-laden fluids are pumped).

In Anglo-Saxon countries the specific speed is called "type number K" in accordance with DIN EN ISO 17769-1 and DIN EN ISO 9906. In the USA it is referred to as N_s (pump specific speed), with the flow rate being specified in gallons/min, the head in foot and the rotational speed in rpm. The conversion factors are:

K = n_s / 52.9 and N_s = n_s ∙ 51.6

The controlled adjustment of rotational speed as it applies to rotating machines and, thus, centrifugal pumps, is also referred to as speed control. Speed control is used on centrifugal pumps to increase their energy efficiency by adjusting pump speed to the actual output (performance data) required.

• Pole pair number
  Special pole-changing motors for two to four speed levels are used. Pole changing leads to sizeable differences in speed in the switching steps, which is why this type of speed adjustment is not very relevant to centrifugal pumps. See Fig. 1 Speed control

• Slip
  Reducing the voltage by means of phase angle control. Realising speed control by varying motor slip creates high slip loss in the rotor. As a result, this method is only practical when very small power ratings are involved (e.g. glandless circulator pumps). See Fig. 2 Speed control

• Frequency
  By means of a frequency inverter. Varying the frequency and voltage of three-phase asynchronous motors is the most common speed control method. This option is highly effective. It requires relatively little investment and provides a high efficiency. See Fig. 3 Speed control

Speed measurements are used to quantify the speed at which a body rotates and can be carried out in different ways.

Methods for measuring speed

• Electromagnetic induction speed transmitter that generates a voltage proportionate to the rotational speed
• Manual tachometer based on the eddy current principle, together with a manual incremental counter at the shaft end of the pump or motor
• Electronic counter (for high accuracy requirements) that receives pulses proportionate to the pump speed as transmitted from the shaft (optical or magnetic signals are most frequently used)
• Slip meter (slip coil or slip magnetic needle) that is positioned at a specific axial distance from the motor

Speed transmitters are also referred to as rotary pulse encoders or incremental transmitters and record the changes in position (distance covered and direction) of defined points (also see Metrology).

The sprinkler pump is used for supplying fire-fighting water and an example of a stationary fire-fighting pump.

The squirrel-cage motor is an asynchronous motor with rotors whose geometry resembles a squirrel cage.

A centrifugal pump's H/Q curve is called stable if it exhibits a continuously negative slope (negative differential quotient from head and flow rate) with regard to the Q axis. See Fig. 1 Stable H/Q curve

Each stage of a multistage centrifugal pump consists of a combination of an impeller with a diffuser element such as a diffuser, a circular casing or volute casing. 

The characteristic feature of a centrifugal pump's stage is the transmission of power from the pump shaft (see Power input) to the fluid handled (see Pump power output). These two factors allow a value for each stage's efficiency to be specified which represents the targeted highest attainable efficiency constant across all stages in multistage pumps, unless adverse inlet conditions or NPSHA values have to be taken into account.

The number of stages (i) of a multistage centrifugal pump should be selected in such a way that hydraulically favourable conditions prevail at the individual stages depending on the type of impeller. In this context, the determining factor for the individual impeller is not the specific speed of the pump (n_s.P), but the specific speed related to the stage (n_s.St).

The standard nozzle is a differential pressure measuring instrument whose geometric dimensions, surface, and installation conditions comply with the requirements specified by standard DIN EN ISO 5167-3 (also see Standard orifice, Standard Venturi nozzle, Venturi tube). 

The standard nozzle has a narrowing, rounded profile (inlet) and a cylindrical throat. The specifications given in DIN EN ISO 5167-3 apply. See Fig. 1 Standard nozzle

The flow volume is calculated based on the differential pressure level measured and the flow coefficient (C) using the formula for differential pressure measuring instruments. The flow coefficient is depicted in a table in appendix A1 of DIN EN ISO 5167-3.

The overall pressure losses of the standard nozzle are less pronounced than those of the standard orifice for the same nominal diameter and diameter ratio. The lengths of the inlet sections correspond to those of the standard orifice.

The standard orifice is also referred to as a measuring orifice or simply an orifice and is a differential pressure measuring instrument. It comprises an orifice plate that is inserted into piping and has a bore hole diverging in the flow direction to measure the flow rate. When a fluid passes through the orifice, a differential pressure is produced (see BERNOULLI) between the measuring points "upstream of the orifice" (positive pressure) and in the "narrowest cross-section" (negative pressure) so that the flow rate can be calculated. See Fig.1 Standard orifice

The term "measuring orifice" is used to make a distinction to an orifice that is used to throttle (see Closed-loop control) the flow rate. With respect to its geometric dimensions, surface quality, and installation conditions (e.g. minimum lengths of straight pipe runs upstream and downstream of orifice), the standard orifice meets the requirements defined by a standard (e.g. DIN EN ISO 5167) that also provides detailed information about measurement accuracy and application limits.

The flow volume is calculated based on the differential pressure level measured and the formula for differential pressure measuring instruments. The flow coefficient (C) is depicted in a table in Appendix A of DIN EN ISO 5167-2:2022-6 (also see Standard nozzle, Standard Venturi nozzle, Venturi tube).

Standard pressure is a globally defined and standardised condition (STP for "Standard Temperature and Pressure") for specifying the properties of fluids (also see Standard temperature and pressure).

The standard signal is a standardised electrical or pneumatic signal used in process automation. For this purpose, a measured value is measured by a sensor, for example, and converted into the standard signal for processing (also see Analog interface).

According to DIN 1343 standard temperature and pressure is a specific state for a solid, liquid or gaseous substance as defined by the standard temperature (T_n) and the standard pressure.

The volume of a substance under standard temperature and pressure is referred to as the standard volume (V_n). The quantity-specific (molar) standard volume of the ideal gas (V₀) is

The standard Venturi nozzle is a differential pressure measuring instrument whose geometric dimensions, surface quality, and installation conditions meet the requirements defined by DIN EN ISO 5167-3. The profile is rotationally symmetric and comprises a cylindrical throat, diffuser and narrowing inlet with rounded profile that are identical to the orifice of a standard nozzle.

See Fig. 1 Standard Venturi nozzle

The flow volume is calculated based on the differential pressure level measured and the flow coefficient (C) using the formula for differential pressure measuring instruments. The flow coefficient is depicted in a table in appendix A3 of DIN EN ISO 5167-3.

The overall pressure losses of the standard Venturi nozzle are considerably lower than with a standard nozzle of the same nominal diameter and diameter ratio. The lengths of the inlet sections, however, correspond to those of the standard nozzle.

Standardised chemical pumps are chemical pumps, with standardised dimensions and hydraulic output (see Standardised pump). Standardised pumps can be replaced with equivalent pumps of any make. Their back pull-out design enables removal of the bearings including shaft seal and impeller without having to disconnect the pipelines from the pump casing.

If a flexible spacer-type coupling is fitted, the motor does not need to be moved in this process, which means the pump set does not need to be re-aligned after its reassembly. See Fig. 2 Back pull-out design and Fig. 5 Shaft coupling

The main standardised chemical pumps used in the chemical and petrochemical industries are in compliance with EN 22858 / ISO 2858 / ISO 5199 or, in the U.S., ASME B 73.1. See Fig. 1 Standardised chemical pump

Apart from complying with standards EN 22858 and ISO 2858, which mainly stipulate the dimensions of a pump, chemical pumps often need to fulfil the specifications laid down in ISO 5199, VDMA 24297 and EN 809. These standards stipulate, for example, the maximum permissible vibrations, shaft deflection, noise levels (see Noise in pumps and systems), safety requirements, pipeline forces and moments to be absorbed (see Pump nozzle load) and specify an installation without foundation. The requirements on baseplates for horizontal pumps with a drive are laid down in standard ISO 3661. See Fig. 12 Pump casing

Standardised pumps are pumps which comply with the requirements, guidelines, directives or recommendations issued by a standards institute, or a manufacturers' or users' association

Abbreviations of national, European and international standards institutes: 

• ACS: American Chemical Society; standardised: American Voluntary Standard (AVS) pump
• AFNOR: Association Française de Normalisation (French standards' institute)
• ANSI: American National Standard Institute
• API: American Petroleum Institute
• ASME: The American Society of Mechanical Engineers
• BPMA: British Pump Manufacturers' Association
• BSI: British Standards Institution
• Codata Committee on Data for Science and Technology (see Standard temperature and pressure)
• DIN: Deutsches Institut für Normung (German standards' institute)
• DVGW: Deutsche Vereinigung des Gas- und Wasserfaches e.V. (German association for gas and water)
• EN: European Standard (CEN Comité Européen de Normalisation)
• ISO: International Organization for Standardization
• VDE DKE: Deutsche Kommission Elektrotechnik Elektronik Informationstechnik in DIN und VDE (German commission for electrical, electronic and information technologies)
• VDI: Verein Deutscher Ingenieure (German association of engineers)
• VDMA: Verband Deutscher Maschinen- und Anlagenbau e.V. (German engineering association)
• VdS: Gesamtverband der Deutschen Versicherungswirtschaft e.V. – GDV (German association of insurance companies)
• UNI: Unificazione Italiana (Italian standards' institute)

A standardised water pump is a standardised pump, which differs by comparison with the standardised chemical pump in its performance, pressure class, shaft seals and materials. These pumps are used predominantly in general industry applications and less frequently in the chemical and refinery industries.

In a star configuration all three phase conductors of a three-phase system are electrically connected at one end. The resulting connection, which forms the centre point, is referred to as star point. 

It is connected to the neutral conductor (N). The free ends are connected to the external conductors (L1, L2, and L3).

The star impeller is a component installed in side channel and liquid ring pumps such as the water ring pump which work on the positive displacement principle. See Figs. 1, 2, 3 Star impeller

Star-delta starting is also referred to as Y-delta or wye-delta starting and describes a starting method that is used for three-phase motors to avoid excessive starting current.

The starting of pumps is referred to as the start-up process.

The start-up process refers the process by which the drive is activated and accelerated until the operating point of the pump is reached. There are several starting methods, to make this stage of operation as low in impact as possible.

The torque (T_p) of the pump that is transferred by the shaft coupling is directly related to power (P) and rotational speed (n). When the centrifugal pump is started up the torque versus speed curve is almost a parabola. The starting torque provided by the asynchronous motor, however, must be greater for the rotor to reach operating speed.

This motor torque, together with the voltage, has a direct impact on the current drawn by the motor and thus also characterises the build-up of heat in the motor winding. Impermissible heat build-up in the motor should be avoided by limiting the run-up time and/or current.

The squirrel-cage motors used for centrifugal pumps (see Asynchronous motor) have high starting currents.

For motor ratings below 4 kW, the DOL starting and soft starting methods are used, while the star-delta, auto transformer, soft starter and frequency inverter methods are preferred for motor ratings above 4 kW.

DOL starting

For DOL starting, the three motor winding connections are wired in delta configuration from the outset. This means that the full mains voltage is immediately applied to the stopped motor, i.e. the entire starting torque is available right from the beginning. The operating speed will be reached within a very short period of time.

This starting method is the most favourable one for the motor, even if the starting current increases to 8 times that of the nominal current. Since this can place a demanding load on the power supply mains when larger motors are involved and cause voltage dips for adjacent devices, it is important to observe the provisions issued by the energy supply companies for DOL starting of motors with ratings above 5.5 kW in public low-voltage mains (400 V).

In actual practice, motors with ratings up to 7.5 kW are also started directly. See Fig. 1 Starting method

Star-delta starting

Star-delta starting is used to drive machines with a high moment of inertia and limit the starting current of an asynchronous motor connected in delta configuration.
For star-delta starting, the armature winding is initially connected to the power supply mains in a star configuration and the motor is brought up to speed in this configuration. At switchover, delta current is theoretically all that is required and corresponds to the current rotational speed.

The result is a reduction in starting current of 1/3 as compared with delta DOL starting. The same relation applies to torque. See Figs. 2, 3 Starting method

Star-delta starting can only be used for three-phase motors whose winding connections are not connected internally, but are routed separately outwards. The delta connection may only be established after the machine has run up to speed in order for the targeted reduction in starting or inrush current to be realised. The torque produced with the star configuration must be sufficient to accelerate the driven machine to about its nominal speed. Switching from star to delta can be effected manually or automatically.

In practice, the star-delta configuration comprises a contactor circuit that allows the motor winding connections to be switched between the external conductors and the star point. Both switching states are interlocked in operation. Automatic switchover is possible if additional control relays are used. See Fig. 4 Starting method

Switching the configuration from star to delta will cause current and torque peaks, which increase the mechanical load placed on coupled components. Very smooth starting and stopping can only be achieved via electronic solutions such as a soft starter or frequency inverter.

Auto transformer

An auto transformer typically finds application in high-powered motors to ease starting. To this end, it reduces the voltage (and thus the starting current) supplied to electric asynchronous motors. The transformation ratio of the transformer further reduces this current by the square of the reduction. Auto transformers are the most frequently used type of starting transformer for cost reasons.

Starting torque is the torque transferred by the shaft coupling during run-up (see Start-up process). It is calculated based on the ratio of power (P) to angular velocity (ω) and is represented as a rotational speed function.

Factors influencing torque:

• Progression of the characteristic curves for the head and pump power input in relation to flow rate and rotational speed.
• Position of the operating point on the characteristic curves
• Run-up behaviour of the drive, as characterised by the run-up time (t_a) of the unit (pump and motor)
• System characteristic curve in relation to the valves fitted
• Run-up time (t_aQ) for accelerating the liquid mass in the filled piping

t_aQ     Run-up time of the liquid mass in the piping in s
Q       Flow rate in m³/s
H₀      Shut-off head (head) in m
H_A,0   Static part of the system characteristic curve in m
g        Acceleration due to gravity in m/s²
L        Length of the piping in m
A        Cross-sectional area of the piping in m²

To illustrate the possible progression of starting torque at low specific speeds, the head (H), power input (P), and starting torque (T_P) of a radial pump are examined under different operating conditions. See Fig. 1 Starting torque

All starting torque curves (T_p) begin with the  breakaway torque (T_PL) to overcome bearing and seal static friction. They reflect the increase in torque along with rising rotational speed (n) and the increase in power input (P) as a function of increasing flow rate (Q). These processes occur either at the same time or in succession.

In contrast to centrifugal pumps with low specific speeds, a different starting torque curve develops at high specific speeds (e.g. propeller pumps) due to the increasing flow rate and decreasing power input (characteristic curve). More starting torque is therefore required for starting against a closed gate valve (points I and II would be located above line A-B) than for starting against empty, unpressurised piping (point III would be located below the operating point (B)). This characteristic must be observed.

Static pressure refers to the pressure that would be measured by a sensor moving along with the fluid. In centrifugal pump engineering, the term pressure is commonly understood to mean a static pressure.

The stator as used in electric motors is a stationary, non-moving part of an electrical machine. It typically doubles as a casing and serves as a joint core for the induction coils. Its counterpart is the rotor.

The flow of a fluid is steady if its velocity, pressure and all the numerical values relating to its substance (e.g. density and viscosity) are independent of time at every point in the flow field. A steady flow is in principle only possible in a condition of equilibrium (steady state).

A turbulent flow is, strictly speaking, a transient flow as the turbulent fluctuations are statistically irregular, time-dependent phenomena. However, a turbulent flow can be treated as a steady flow with reasonable accuracy, if the time-averaged values of velocity, pressure etc. are taken into account.

The same applies to the absolute velocity within, and in close proximity to, the impellers of centrifugal pumps, which in the strict sense is (periodically) transient due to the finite number of vanes. However, when the values averaged over time are taken into to account, it can be considered steady.

The stop pressure indicates when a pump has to be switched off because it has exceeded the required operating pressure due to a pressure increase, for instance.

The term "straight length of piping" is primarily used in metrology, i.e. when measuring flow rates by means of throttling devices (e.g. standard orifice, standard nozzle, standard Venturi tube).

As a rule, a straight length of piping must be available upstream and often also downstream of each pressure or velocity measurement point, if a defined measurement accuracy (see Measurement uncertainty) needs to be achieved.

A straight length of piping is also required upstream of the pump suction nozzle to ensure the centrifugal pump's operating behaviour is optimal.

This holds particularly true for pumps with a high specific speed (see Inlet conditions).

Straight-way valves are distinguished from other globe valve types by their geometry, i.e. their inlet and outlet ports are arranged in the same axis (also see Valve).

Strain gauging in the context of centrifugal pumps is used primarily to determine the strength of pump casings and impellers as well as to measure axial thrust, torque (see Power measurement) and the torsional strain of pump shafts. To take extension measurements, strain gauges (SGs) are fixed (glued/bonded, welded) to the component in question.

In a flow, the stream line is a line whose local direction corresponds to the direction of the local flow velocity. 

In steady flows where a velocity independent of time exists at every point within the flow space the stream line describes the path of a given liquid particle (particle trajectory or path line).

Stream lines exhibit no breaks and can never intersect with one another, as otherwise two different flow velocities would have to occur at one and the same point. See Fig. 2 Vane cascade

As it is not possible to have normal velocity components along a solid wall, such as an impeller vane or pump casing, it follows that all the body contours of the flow space are simultaneously stream lines.

Strictly speaking, the Bernoulli equation which is often applied in fluid mechanics, ​​​​​​​is only valid for various points on a common stream line. However, often the equation is also used for a flow space designated the "thread of stream or filament of flow" which is enclosed by all the stream lines passing through a continuous line.

In the case of fluid flow in pipes, the entire liquid content of the pipe is usually considered to be a filament of flow (see Flow velocity in a cross-section).

The circular projection of a stream line into the meridional section plane (section through the axis of rotation) of an impeller is referred to as flow line.

Stress corrosion cracking is a type of corrosion, that causes cracks with intercrystalline (along the grain boundary of the microstructure) and transcrystalline (within the grain) propagation to form in metals due to the effects of certain corrosive media at purely static or superimposed dynamic low-cycle mechanical stresses. These may also already be inherent in the workpiece in the form of tensile stresses.

Characteristic of stress corrosion cracking is separation with low-level deformation, often occurring without the formation of any visible corrosion products. A causal distinction is made between electrolytic (anodic) and hydrogen- or elongation-induced cracking. See Figs. 1 and 2 Stress corrosion cracking

A stripping system is an auxiliary device on cargo oil pumps which enables the continuous discharging (unloading) of oil from tankers to take place without any manual intervention right up to the end of the discharging operation. The purpose of the stripping system is to prevent the breaking off of the flow by gas intrusions into the suction pipe, such as those that occur during residual pump-out operations.

The Strouhal number is defined as follows:

w     velocity of flow around a body (for propellers, the relative velocity at the impeller outlet is used) in m/s
f      vortex-shedding frequency (sought excitation frequency) in s^-1
d     characteristic quantity of the separating vortices (thickness of profile surrounded by the flow) in m

The dimensionless number plays an important role in hydro-acoustics and characterises transient flow phenomena in all cyclically operating prime

Sr = 0.2 to 0.24 (flow along the plate)

Submersible borehole pumps are a type of submersible pump. They are centrifugal pumps driven by a submersible motor. As they usually draw in the fluid directly without a suction line, they must constantly be submerged in the fluid handled.

Submersible borehole pumps are designed as single-stage or multistage pumps which are rigidly coupled to the submersible motor. The motor can be arranged on top or underneath the pump, depending on the application. 

They are employed as submersible borehole pumps for use in tank farms and a cavern pumps, for example. Their most common application is that of a borehole pump Borehole pumps are more cost-efficient than deep-well turbine pumps, especially for large installation depths, as their rising mains have a simpler design. See Fig. 1 Submersible borehole pump

To meet the typical conditions of a borehole, submersible borehole pumps are designed with a small diameter and a large axial length. 

The motor, which is usually installed underneath the hydraulic stages, is a water or oil filled squirrel-cage motor (e.g. submersible motor), which is sealed off from the pump by a mechanical seal or another similar shaft seal. A suction strainer is fitted between the pump and the motor.

As the pump set is inaccessible during operation it must be entirely maintenance-free. Particular attention must be paid to the bearings absorbing radial and axial forces. The plain bearings which are lubricated by the fluid handled or the motor fill, are commonly made of carbon, bronze, synthetic resin-impregnated hard fabric, ceramic or hard metal.
Depending on the requirements, the pump casing, impellers and diffusers are made of cast iron, bronze, aluminium multi-alloy bronze, chrome nickel steel or plastic.

A check valve (see Valve) is fitted at the very top of the pump set. The fluid handled (see Flow rate) is guided through this valve to the riser, from which the entire pump set is suspended.

The power cable is routed out of the motor through a cable gland and up along the outside of the pump and inside the riser to the top.

The principal applications of submersible borehole pumps are irrigation, maintenance of groundwater levels in open-cast and underground mining or construction pits, pumping tasks in water-supply wells and in the offshore, geothermal energy or deep-sea mining sectors.

The pump sets have to be matched to each application, especially when the fluid to be handled contains sand and contaminants.

Submersible borehole pumps for use in tank farms are submersible borehole pumps which are used for tank farm applications (see Cavern pump).

A submersible mixer is a mixing unit consisting of an open axial propeller and a dry submersible motor (also see Mixer). 

A submersible motor is an asynchronous squirrel-cage motor wetted on the outside and inside, i.e. it is completely immersed in the fluid handled and filled with liquid. It is used as a drive for usually vertical, multistage pumps in boreholes, shafts, wells, containers or open waters, and, unlike the air-filled submerged motor (see Submersible motor pump) is suitable for immersion depths of up to several kilometres (see Submersible borehole pump). See Fig. 1 Submersible motor

The slim design necessary for its use in boreholes substantially reduces the power loss of the rotors in the liquid (see Disc friction), which in rotating cylinders increases by the fifth power of the diameter.

The liquid in the motor lubricates the plain bearings of the rotors. The stator windings must be insulated by fluid-resistant plastics (wet winding) if they are not protected by a can (see Canned motor pump). 

The heat produced by the submersible motor is dissipated into the surrounding fluid handled.

Submersible motors have a power range of up to 3500 kW, with operating voltages up to 10 kV for large motors.

Submersible motor pumps are pumps driven by an asynchronous motor. Their hydraulic components (pump casing, impeller, diffuser element) and motor are flooded by the fluid handled.

Submersible motor pumps are installed by being lowered into the pump sump along a guide wire or guide rail arrangement. The pump claw with a rubber profile seal inserted attaches itself almost leakage-free to the piping permanently installed in the pump sump, so that the pump set can be fully flooded. The motor heat is dissipated via the motor housing to the fluid surrounding it.

Submersible motor pumps with liquid-filled motors (e.g. submersible motors) are suitable for operation at any installation depth. Submersible motor pumps can also have air-filled (or less frequently oil-filled) submersible motors which are designed for low to medium installation depths (of up to 80 m). In certain cases, these motors only need to be occasionally or partly submerged in the fluid handled as the motor heat is dissipated to the fluid handled by means of heat conduction and to the atmosphere via the large surfaces of the motor housing by convection or forced air flows.

Applications of vertically installed submersible motor pumps
See Fig. 1 Submersible motor pump

• Fighting floods
• Transporting waste water (See Figs. 2, 3, 5 Waste water pump)
• Drainage (See Fig. 2 Drainage pump and Fig. 2  Pump for use in low-lift pumping stations)
• Irrigation (See Fig. 1 Irrigation pump)
• Cooling (See Fig. 5 Cooling water pump)
• Water disposal (See Waste water lifting unit)

Submersible motor pumps are usually designed as single-stage pumps. They generally do not require a suction line, as the fluid to be handled approaches the pump from all sides. Smaller pump sets are transportable and usually fitted with a level-controlled switch starting and stopping the pump set automatically.

The materials of submersible motor pumps have to be specifically selected for the fluid to be handled and the sand or contaminants it may contain. The pumps can also be designed with explosion protection.

Submersible pumps are centrifugal pumps whose hydraulic components (pump casing, impeller, diffuser element) are flooded by the fluid handled. Usually, this type of pump is not fitted with a suction line.

A submersible pump whose motor is arranged above floor is referred to as a vertical shaft submersible pump. 

This type is typically used as

• irrigation pump see Fig. 2 irrigation pump,
• deep-well turbine pump,
• chemical pump see Fig. 4 chemical pump
• drainage pump see Fig. 1 drainage pump
• cooling water pump see Fig. 1, 2, 3, 6, 7 cooling water pump,
• tubular casing pump,
• pump for use in low-lift pumping stations see Fig. 1 pump for use in low-lift pumping stations
• tank farm pump.

IPumps whose motor is flooded in addition to the hydraulic components are referred to as submersible motor pumps.

This type of pump is used as a

• waste water pump   see Fig. 2, 3 und 5 waste water pump
• irrigation pump see Fig. 1  irrigation pump
• drainage pump see Fig. 2 drainage pump,
• cooling water pump see Fig. 5 cooling water pump,
• tubular casing pump
• Pump for use in low-lift pumping stations see Fig. 2 Pump for use in low-lift pumping stations

The same principle is used for submersible borehole pumps.

A submersible pump in discharge tube consists of a centrifugal pump and a submersible motor. The fluid handled flows through the impeller in axial direction. The pump is suspended directly in the discharge tube. See Fig. 1 Submersible pump in discharge tube

These pumps are usually installed vertically; in special cases they can also be installed in an inclined or horizontal position.

Submersible pumps in discharge tubes are not self-priming, which means that the propeller (as an axial impeller) always has to be sufficiently covered by the fluid handled. This is why wet well installation is typically chosen. The top of the intake chamber can be open or covered.

Depending on the specific speed, the impeller is designed as an axial flow impeller, mixed flow impeller or channel impeller. When the pump is installed, its diffuser ends directly in the discharge tube, which can be designed with an elbow for above floor or underfloor discharge, or as an overflow version.

Regardless of the type of installation and the discharge tube design, the surface-cooled dry-rotor submersible motors (see submersible motor pump) of submersible pumps in discharge tubes are permanently cooled by the fluid flowing along the motor during operation.

Submersible pumps in discharge tubes are suitable for applications which cannot be covered by conventiona tubular casing pumps or vertical shaft submersible pumps. 

One of their benefits is that structural work is kept to a minimum. Submersible pumps in discharge tubes are usually installed underfloor with the submersible motor pump suspended in a discharge tube made of concrete, sheet steel, or increasingly also of GFRP (Glass Fibre Reinforced Plastics).

The actual outlet line is arranged underneath the floor on which the discharge tube is placed. A building above this arrangement is not required.

Mobile lifting equipment is used for installation and removal.

The benefits of this simple building design, easy installation, maintenance and repair increase with the depth of the discharge tube and the installation depth of the pump. Submersible pumps in discharge tubes can easily be pulled out as a single unit. This sets them apart from conventional tubular casing pumps or deep-well turbine pumps, which require a complex and time-consuming disassembly of drives, shaft assemblies and discharge pipe.

Installation variants for a discharge tube with open overflow, for example, can only be realised with submersible pumps in discharge tube design. Axial flow impellers (e.g. propellers) reach heads of up to 12 m, mixed flow propellers up to 55 m and channel impellers up to 30 m.

Hydraulic systems with axial flow or mixed flow impellers can pump very high flow rates of 10 to 20 m³/s. The performance range of propeller pumps is decisive for matching them to their applications.

Main applications of propeller pumps

• Irrigation and drainage pumping stations
• Waste water treatment plants and stormwater stand-by tanks
• Raw and clean water pumps in water works
• Cooling water pumps in power stations and industry
• Industrial water supply
• Flood, disaster and water pollution control
• Pumps for docks and locks
• Fish farms/aquaculture
• Leisure park water attractions
• Transporting and recirculating fluids in environmental and plant engineering projects

The suction casing on ring-section pumps with radially split casings is a portion of the pump casing which is designated according to its function. The suction casing is the first of several so-called stage casings which are arranged in tandem. Tie bolts ensure pressure-tight connection of the individual stage casings.

A centrifugal pump's suction characteristics describe the pump's reaction to changing NPSHa values (NPSH of the system) at the operating point and are determined by cavitation on the pump system's suction side and in the pump itself. A centrifugal pump can be operated continuously at the rotational speed (n_contract), flow rate (Q_contract) and head (H_contract) and with the fluid specified in the supply contract if NPSHa is greater or equal NPSHr (= NPSH required by the pump), i.e. if

In a pump operating at a given operating point characterised by a flow rate (kept at a constant value) and a pump speed (kept at a constant value), a decrease in NPSHa is accompanied by a more or less pronounced decrease in head as a result of cavitation. 

A common method of evaluating the suction characteristics is to plot the flow rate or pump efficiency (η) against NPSHa.

The suction coefficient (S) introduced by Pfleiderer – but no longer used – is a characteristic coefficient for the evaluation of the net positive suction head (NPSH) of a centrifugal pump's impeller.

S is defined as:

The suction coefficient for axial flow impellers is approx. 2.5 and for radial impellers approx. 3.0. Special designs can achieve much higher suction coefficients.

In accordance with international standards, the suction specific speed n_ss is used nowadays to describe the suction characteristics of centrifugal pumps.

The suction elbow is also referred to as intake elbow.

The term suction eye designates the inlet cross-section of an impeller.

The suction head is the geodetic height of a liquid level above the impeller inlet. See Geodetic positive suction head