Affinity laws

When investigating flow phenomena, cost factors often favour the use of models which are geometrically similar to the original, full-sized equipment (see Similarity conditions).

 For this type of testing it is necessary that models are not only geometrically similar, but are also subjected to similar physical conditions.

The physical laws (differential equations including boundary conditions) applied must remain invariant under similarity transformations. This is achieved by dividing all relevant physical quantities by exponential products characteristic of the configuration to be tested so as to obtain ratios of the unit 1.

Physical similarity is achieved if the ratios (see Characteristic coefficient)

of the original and the model are the same. The relationships established between the physical quantity of the original and that of the model by means of the characteristic coefficients are called affinity laws.

Using characteristic pump parameters such as the impeller diameter (D), rotational speed (n), acceleration due to gravity (g) and the density of the fluid handled (ρ), various characteristic coefficients can be established for a centrifugal pump assuming frictionless, incompressible, non-cavitating flow.

Establishing characteristic coefficients by means of the affinity laws:

• Flow velocity (v / (n · D)) 
• Pressure (p / (ρ · n² · D²)) 
• Specific energy (Y / (n² · D²)) 
• Head (g ·  H / (n² · D²)) 
• Flow rate (Q / (n · D³)) 
• Power input (P / (ρ · n³ · D⁵)) 

The following model laws thus apply to two geometrically similar centrifugal pumps operating under physically similar conditions:

Affinity laws

• Flow velocity in a cross-section
  
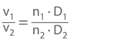
• Pressure

• Specific energy
  

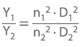
• Head
  

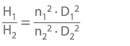
• Flow rate
  

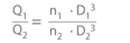
• Power input (assuming identical pump efficiencies)

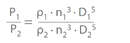
• Flow coefficient

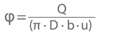
• Head coefficient

  
  

If Δh_s = Y (see Specific energy)  is inserted, the pressure coefficient in its known form can be established:

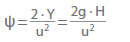
As pump efficiencies are more or less dependent on friction conditions, they are subject to other conversion laws (see Efficiency scale-up). The selection of characteristic quantities to determine the characteristic coefficients is largely arbitrary. For instance, when studying the theory of flow in radial impellers (see Impeller) , the impeller's  circumferential speed (u), its outlet diameter (D) and the outlet width (b) of the vane passage are selected as characteristic quantities. These are used to establish two characteristic coefficients, where Δhs is the isentropic increase (see Entropy) ) of the generalised specific enthalpy of the fluid handled.

As a general rule, a length (l) and a velocity (v) are selected as characteristic quantities for flow investigations. Flows subject to friction are characterised by the kinematic viscosity (ν). The Reynolds number (Re), can be derived from these and also gives the ratio of inertia force to friction force.

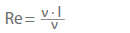
If gravity has to be taken into account as an external force, the characteristic coefficient of the acceleration due to gravity is g · l / v2. Its reciprocal value is the Froude number (Fr). 

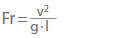
It expresses the ratio of inertia force to the force of gravity. If further physical phenomena such as compressibility, heat transfer and surface tension etc. have to be taken into account, further characteristic coefficients must be introduced.

As characteristic coefficients are not independent of one another, it becomes impossible to achieve physical similarity when multiple characteristic coefficients require consideration.

Model tests are widely used to investigate fluid mechanics, design strength and heat transfer problems.