Affinitätsgesetz
Das Affinitätsgesetz ist ein Spezialfall der Modellgesetze und besagt, dass die Drosselkurven für verschiedene Drehzahlen in der üblichen Darstellung durch folgendes Gesetz auseinander hervorgehen:
Wenn PQ =ρ · g · Q · H (siehe Förderleistung) und P = PQ / η (siehe Leistungsbedarf), ergibt sich unter Annahme einer unveränderlichen Dichte (ρ) des Fördermediums und eines konstanten Pumpenwirkungsgrades (η) entsprechend:
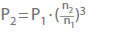
Äquivalente Punkte der Drosselkurven bei verschiedenen Drehzahlen liegen auf Parabeln mit dem Scheitel im Nullpunkt des QH- und QY-Koordinatensystems. Für diese Punkte gilt, dass die Geschwindigkeitsdreiecke zueinander ähnlich sind.
Da zu verschiedenen Drehzahlen verschiedene REYNOLDS-Zahlen (siehe Ähnlichkeitsbedingungen) gehören, ist eine physikalische Ähnlichkeit der Reibungseinflüsse nicht zu erreichen.
Das Affinitätsgesetz gilt daher exakt nur für ein reibungsfreies, inkompressibles (keine Änderung der Dichte bei konstanter Temperatur und Druckveränderung) und nicht kavitierendes Fördermedium (siehe Kavitation).
Mit Änderung der Drehzahl verschiebt sich auch der Betriebspunkt.
